Machine/Statistical Learning

Mixed

Author

Sungkyun Cho

Published

November 28, 2024

Load packages

# numerical calculation & data frames
import numpy as np
import pandas as pd

# visualization
import matplotlib.pyplot as plt
import seaborn as sns
import seaborn.objects as so

# statistics
import statsmodels.api as sm

# pandas options
pd.set_option('mode.copy_on_write', True)  # pandas 2.0
pd.options.display.float_format = '{:.2f}'.format  # pd.reset_option('display.float_format')
pd.options.display.max_rows = 7  # max number of rows to display

# NumPy options
np.set_printoptions(precision = 2, suppress=True)  # suppress scientific notation

# For high resolution display
import matplotlib_inline
matplotlib_inline.backend_inline.set_matplotlib_formats("retina")

\(f\): \(X_1, X_2, ..., X_p\)가 \(Y\)에 관해 제공하는 systematic information; unknown function
\(Y = f(X_1, X_2, ..., X_p) + \epsilon\), \(Y \perp\!\!\!\perp \epsilon\)
\(\epsilon\): 불확실성의 소스들; reducible error & irreducible error
(epistemic uncertainty & aleatory uncertainty)

\(f\)에 대한 estimate, \(\hat f\)을 구하여,
관측된 \(X_1, X_2, ..., X_p\)로 \(Y\)를 예측하고자 함. 즉, \(\hat Y = \hat f(X_1, X_2, ..., X_p)\)
\(Y - \hat Y\): 예측 오차

앞서 선형모형은 \(f\)를 \(X\)의 선형함수인 parametric model로 가정한 후 parameter를 추정하여 문제가 단순하였으나,
이번에는 \(f\)의 형태를 가정하지 않고, \(f\) 자체를 추정하고자 하는 매우 광범위한 문제임.

예를 들어,

\(X_1, X_2, ..., X_p\): 환자 혈액 샘플의 특성들
\(Y\): 특정 약물에 대한 환자의 이상 반응 위험을 나타내는 변수
\(\epsilon\): 약물 제조상의 차이, 해당 날짜에 환자의 전반적인 컨디션 등

용어 정리

변수들 간의 관계에 있어서, 예측에 사용되는 변수(X)와 예측되는 변수(Y)를 구분하기 위해 여러 용어들이 사용됨.

X: feature, predictor, independent variable
Y: target/label, response, dependent variable, outcome variable, criterion

관측치(데이터의 행): example, instance, observation, record, data point, case

왜 분석하는가?

The Occam’s Dilemma?

예측(prediction)
추론(inference)/해석(interpretation)

정보 획득(information)의 관점에서: Leo Breiman 글 참고

어떻게 \(f\)를 추정하는가?

모수적(parametric) 접근

모수적 접근: \(f\)의 형태를 가정하고, 그 형태에 대한 parameter를 추정
가령, 선형성을 가정한 linear model: \(f(X) = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_pX_p\)
모델을 관찰된 데이터에 fit(적합) 또는 train(훈련) 시켜, parameter(모수) 추정
전형적으로 (ordinary) least squares 방법을 사용
상대적으로 적은 수의 데이터로도 추정이 가능
해석을 통해 변수 간의 관계 추론 용이
\(f\)의 형태를 잘못 가정하면, 잘못된 결과를 낼 수 있음

Source: p.21, An Introduction to Statistical Learning with Applications in Python

비모수적(non-parametric) 접근

\(f\)의 형태를 가정하지 않음
보통, 예측의 정확성이 높도록, 즉 데이터와 최대한 가까운 매우 복잡한 형태의 \(\hat f\)를 추구
과적합(overfit)이 되지 않도록, 새로운 데이터에도 잘 일반화되도록 sweet spot을 찾아야 함
매우 많은 데이터가 요구됨
해석은 어려우나, \(f\)로부터 다양한 정보(information)을 추출하는 방법을 고안
모수가 없을 수도, 있을 수 있으나, 해석 가능한 모수라고 보기 어려움

Source: p.22, An Introduction to Statistical Learning with Applications in Python

The tradeoff between flexibility and interpretability

Source: p.22, An Introduction to Statistical Learning with Applications in Python

어떤 기준으로 이 tradeoff의 수준을 결정할 것인가?

해석에 중심을 두고, 변수 간의 관계를 추론하고자 하는 경우: 모형이 틀릴 위험이 존재 >> bias가 높아짐
예측의 정확성에 중심을 두는 경우: 과적합이 될 위험이 존재 >> variance가 높아짐
이 둘이 항상 대치되는 것은 아님; 단순한 모형이 새로운 데이터에서 더 나은 예측 정확도를 가질 수도 있음!

회귀(regression) vs. 분류(classification)

보통 \(Y\)가 연속형 변수인 경우, 회귀(regression) 문제로 다루고, \(Y\)가 범주형 변수인 경우, 분류(classification) 문제로 일컬어 짐.
회귀모형을 확장하여 확률(연속값)을 구한 후, 이를 이용해 분류문제를 다룰 수 있음; ex. logistic regression
예측 변수의 경우, 연속인지 범주형인지는 상관없음.

Decision Theory

Source: Deep Learning: Foundations and Concepts by Bishop, C. M. & Bishop, H

\(Y = f(X) + \epsilon\)

앞서 선형 회귀 모형에서 구한 것은, conditional probability \(p(Y|X)\)를 모델링 한 것이었음.
이 분포를 Gaussian:\(N(\mu, \sigma^2)\)으로 가정하고, 분포의 평균과 표준편차를 likelihood가 최대가 되도록 추정하는 간단한 모델로 축소했음; predictive distribution

분포 \(p(Y|X)\)를 통해 예측의 불확실성을 파악할 수 있음
만약, 주어진 \(X\)에서 대해 예측값 \(f(X)\)을 하나 결정하는데, 실제 true 값을 \(y\)라고 하면,
그 오차에 대해 발생되는 어떤 penalty 또는 cost를 정의; loss function
loss function을 통해 “최적”의 예측값에 대한 기준을 제공
\(f(x) = E(Y|X=x)\)로 예측하는 것이 많은 경우 적절하지만 일반적으로 그런 것은 아님

Loss/Cost Function

Loss function: \(L(y, f(x))\)
\(y\): true value, \(f\): predicted value

이 loss를 최소화하는 것이 목표
True \(y\)를 모르기 때문에, 평균치인 expected loss를 최소화하는 것이 목표
즉, \(E(L) = \displaystyle \iint L(y, f(x))p(x, y) dx dy\)를 최소화하도록 예측값(\(f\))을 결정
- 각 \(x\)에 대해 \(\displaystyle \int L(y, f(x))p(y|x)dy\)를 최소화
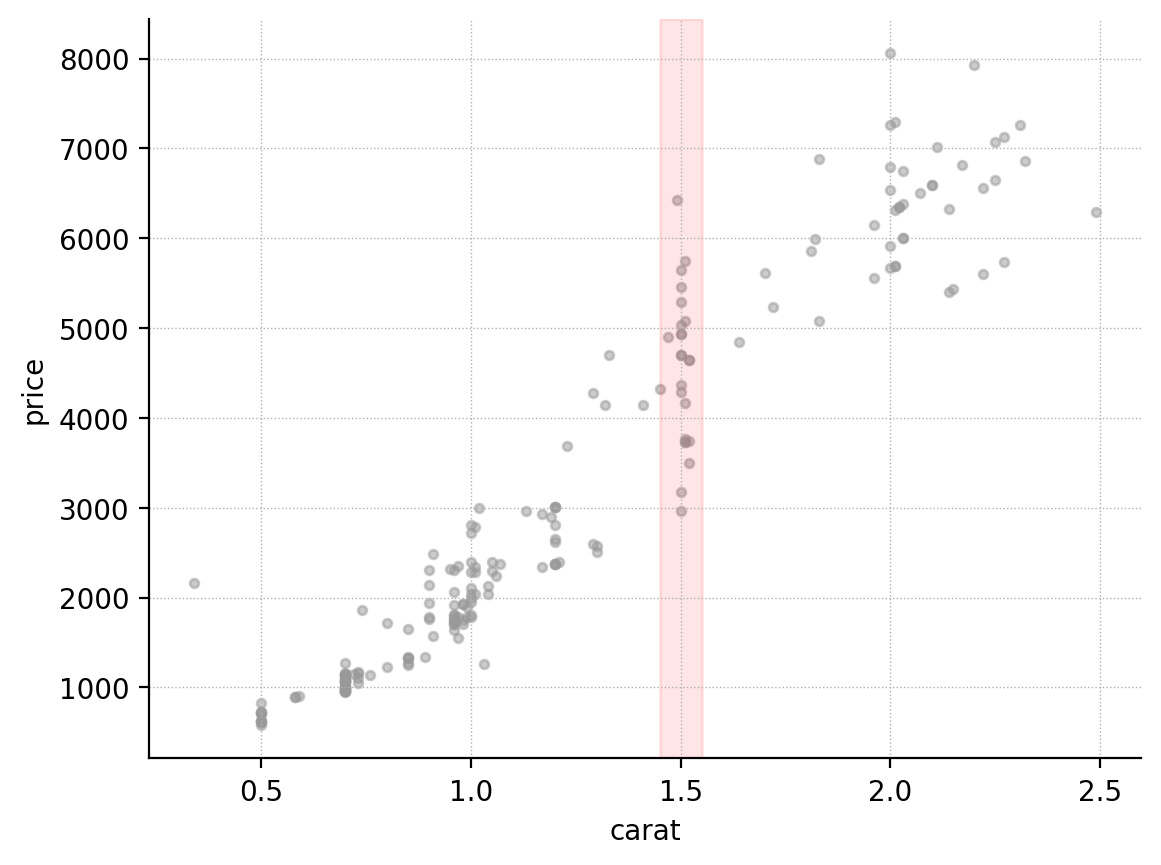
예를 들어, 다이아몬드의 무게로 가격을 예측한다면: 1 carat 다이아몬드의 true price?
또는, 목소리(특정 frequency)로 성별을 예측한다면; 분류 문제의 경우 뒤에서 다룸

Source: Language Log

앞서 회귀 모형에서는 기본적으로 squared loss 사용;

\(L_2 = \displaystyle(f(x) - y)^2\)
- \(E(L)\)을 최소로 하는 함수: \(f(x_0) = E(Y|X=x_0)\): regression function
\(L_1 = \displaystyle |~f(x) - y~|\)
- \(E(L)\)을 최소로 하는 함수: \(f(x_0) = median(Y|X=x_0)\)
\(L_q = \displaystyle |~f(x) - y~|^q\)

Source: Pattern Recognition and Machine Learning by Christopher M. Bishop

예를 들어,

\(f(1.5) = E(Y|X=1.5)\)인 \(f\)가 \(E(L_2)\)를 최소화하는 optimal한 함수임.
즉, conditional mean \(f(x) = E(Y |X = x)\)는 \(L_2\) loss의 관점에서 최적의 함수이며, regression function이라고 부름.

실제로는 \(E(Y | X=x)\)를 계산하는 것은 불가능하며, 이를 추정하기 위해 x의 근방에서 평균값을 취함.

\(\hat f(x) = Ave(Y |X \in N(x))\)

단, 관측치의 수에 대해 상대적으로 predictor의 갯수가 늘어남에 따라 점차 효율성이 떨어짐; the curse of dimensionality
- 예를 들어, 다이아몬드 가격을 carat, cut, clarity의 세 변수로 예측하는 경우,
- \(\hat f(1.5, Fair, I1) = E(Y|carat=1.5,~ cut=Fair,~ clarity=I1)\)

\(f\)의 smoothing에 대한 여러 접근이 있음

regualization, spline, kernel 등

The Palmer Archipelago penguins 데이터셋의 예로 보면,

Artwork by @allison_horst

만약, 부리의 길이로 부리의 깊이를 예측한는 모형에 대해 \(\hat f\)를 구한다면,

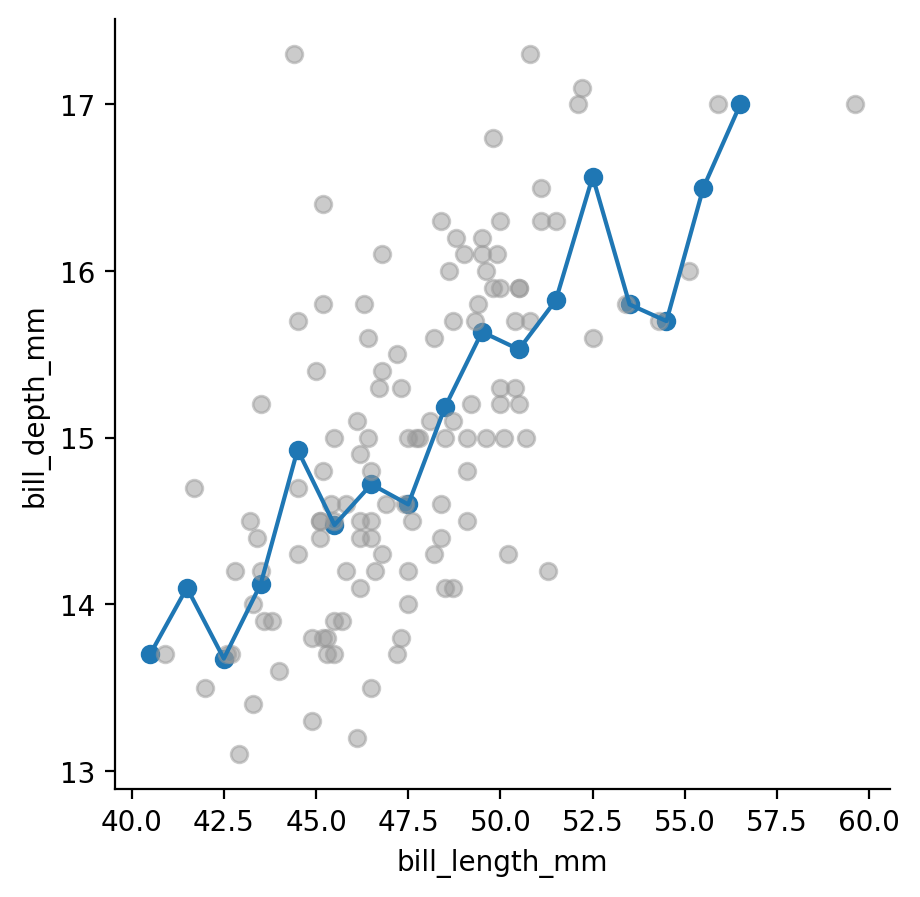
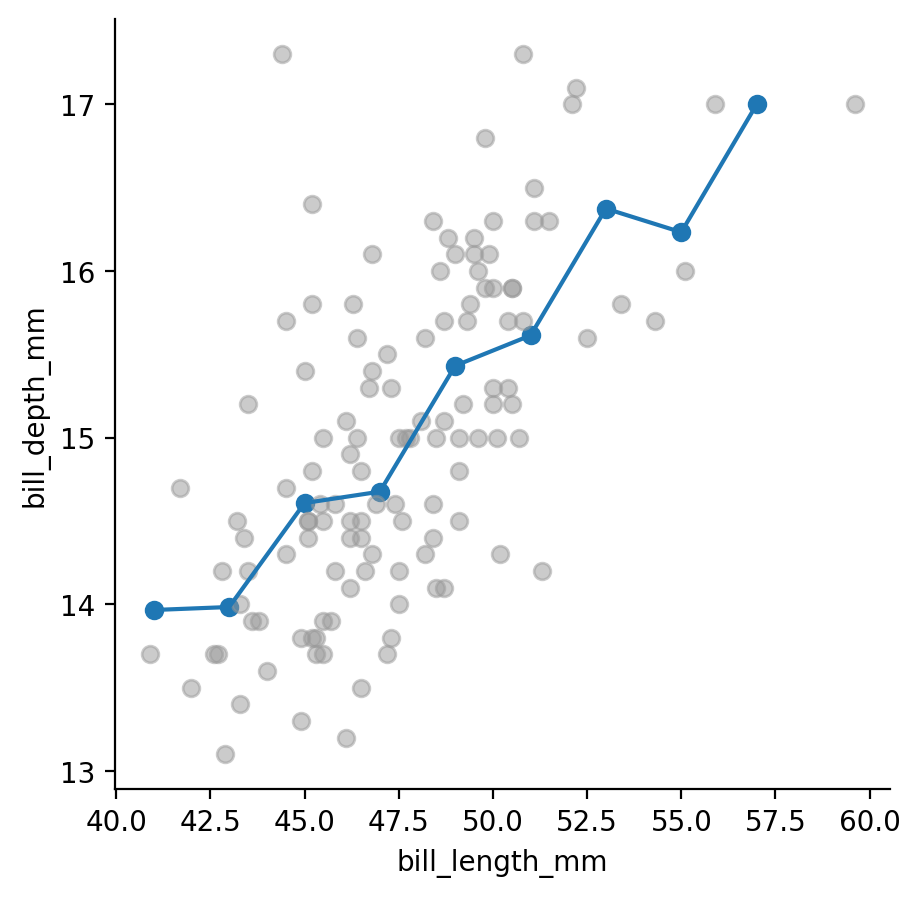
앞서 선형회귀모형을 사용한다면,

관계를 선형이라고 전제하고,
Error가 Gaussian 분포를 따른다고 가정하고,
Likelihood가 최대가 되도록 파라미터(기울기와 절편)를 구한 것임; maximum likelihood estimation
squared error를 최소화하는 것과 동일함.

Source: Visualizing a multivariate Gaussian

Expected value

\(X: \{a, b, a, a, b, c\}\)
The mean of \(X=\displaystyle \frac{a + b + a + a + b + c}{6} = \frac{3*a}{6} + \frac{2*b}{6} + \frac{1*c}{6}=a*\frac{3}{6} + b*\frac{2}{6} + c*\frac{1}{6}\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~=a*p(X=a) + b*p(X=b) + c*(X=c)\): weighted average

Expectation: \(E(X)=\displaystyle \sum x_i p(X=x_i)= \sum xp(x)\)

연속값이라면, \(E(X)=\displaystyle \sum \Delta x * p(\Delta x) = \int x f(x) dx\), where \(f(x)\) is the probability density function
\(p(\Delta x) = f(x)\Delta x\)

The Bias–Variance Trade-off

위의 논의는 특정 데이터셋에 의존할 수밖에 없는데, (참고: Bayesian의 경우 다른 접근)
데이터셋마다 다른 \(\hat f\)를 얻게 된다는 점을 감안했을 때, \(\hat f\)의 변동성을 살펴보면,

\(L_2\) loss의 경우,

\(\displaystyle h(x) := E(Y|X=x)\): optimal prediction of \(Y\) at any point \(x\)
\(~~~~~~~~~ = \displaystyle \int y \cdot p(y|x)dy\)

\(E(L_2) = \displaystyle \iint \left( f(x) - y \right)^2 p(x, y) dxdy = \iint \left( f(x) - h(x) + h(x) - y \right)^2 p(x, y) dxdy\)
\(~~~~~~~~~~~ = \displaystyle \int \left( f(x) - h(x) \right)^2 p(x) dx + \iint \left( h(x) - y) \right)^2p(x, y) dxdy\)

두 번째 항: optimal prediction \(h(x)\)가 true value와 얼마나 떨어져 있는가?(분산) - irreducible error
첫 번째 항: \(h(x)\)와의 차이를 최소화하도록 \(f(x)\)를 선택하는데 하는데, 유한한 데이터셋에서는 그 간극이 존재
- 이제, 분포 \(p(x, y)\)로부터 수많은 데이터셋들 \(D_i\)를 얻었다고 가정했을 때,
- 특정 \(x_0\)에 대해서

\(E_D[\left( f(x_0; D_i) - h(x_0)\right)^2]=[E_D\left( f(x_0; D_i)\right) - h(x_0)]^2 + E_D[\left\{f(x_0;D_i) - E_D\left(f(x_0;D_i)\right)\right\}^2]\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = bias^2 + variance\)

Bias: 최적의 예측값(\(h\))에 비해, (여러 데이터로부터 얻은) “평균적인 예측값”이 얼마나 차이가 나는가?

즉, 최적의 예측보다 평균적으로 얼마나 틀린 예측을 하는가?

Variance: 각 데이터로셋에서 얻은 예측값이 (여러 데이터셋에서 얻은) “평균적인 예측값”에서 얼마나 떨어져 있는가?(분산)

즉, 데이터셋에 따라 \(f(x_0;D_i)\)가 얼마나 민감하게 변하는지 측정

모든 \(x\)에 대한 것으로 비용의 총합으로 확장해서 이해하면,

Expected Loss 분해

\(\displaystyle E(L_2) = (bias)^2 + variance + noise\)

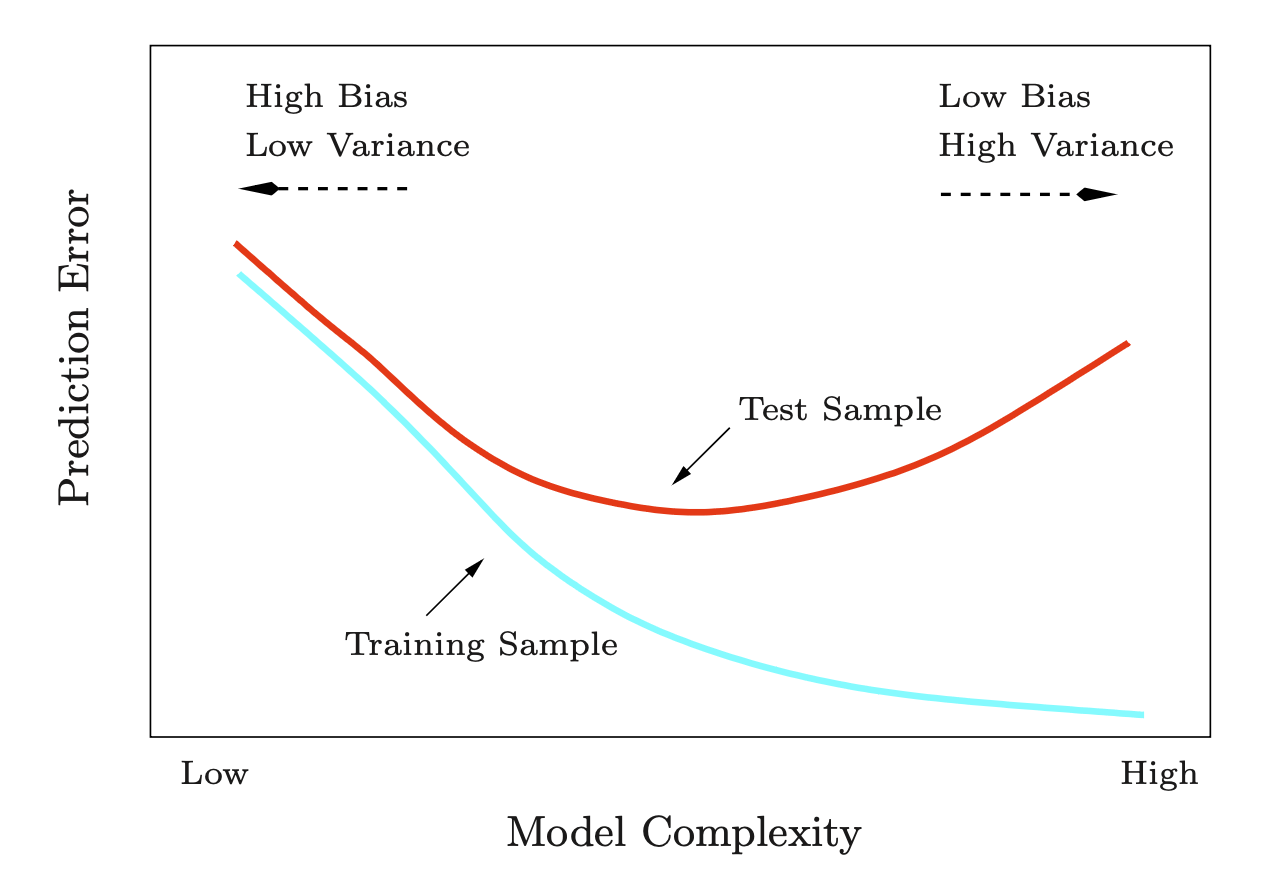
Bias와 variance간에는 trade-off가 존재함

Flexible한 모델의 경우 데이터에 더 잘 적합하여, variance가 높아짐. 즉 데이터셋마다 너무 다른 예측을 하게 됨
- 데이터에 overfitting이 된다고 말할 수 있음.
- 단, N이 증가하면(데이터셋 사이즈가 커지면), flexible한 모델의 variance가 줄어듦.
- 여러 데이터셋으로부터 평균을 얻으면, 실제값에 가까워짐.
Rigid한 모델의 경우 데이터셋에 덜 적합하여, bias가 높아짐. 즉, 평균적으로 더 틀린 예측을 하게 됨
- 한편, 데이터셋에 덜 민감하여 variance가 줄어듦
- 작은 데이터셋에서 더 유리
이 둘의 적절한 균형을 갖는 모델이 최적의 예측 모델임

예를 들어, 함수 \(h(x) = sin(2\pi x)\)로부터 생성된 데이터셋(N=10)에 대해 다항식의 차수에 따른 flexibility의 변화에 따른 OLS 모델들을 비교하면,

데이터셋의 사이즈가 커지면, (M=9인 경우)

함수 \(h(x) = sin(2\pi x)\)로부터 생성된 100개의 데이터셋(각 N = 25)에 대해 3가지 flexibility에 대한 모델들을 비교하면,

Source: p.10, 12, 127, Deep Learning: Foundations and Concepts by Bishop, C. M. & Bishop, H

Classification

\(Y\)가 범주형 변수인 경우, 즉 분류(classification) 문제인 경우

Y가 k개의 범주/클래스로 나뉘는 경우: \(Y \in \{C_1, C_2, ..., C_k\}\)
- 두 범주의 경우, 간단히 \(Y \in \{0, 1\}\)
\(f(x_i): P(Y = C_k|X=x_i)\)가 최대인 클래스에 할당; \(\underset{k}{\mathrm{argmax}}~ P(Y = C_k|X=x)\)
- Conditional class probabilities
- Bayes classifier: 최대치
이 \(P(Y = C_k|X=x)\)를 추정하기 위한 다양한 방식들이 존재
- K-nearest neighbors
- Logistic regression
- Generalized additive models
- Linear/Quadratic discriminant analysis

한 개의 예측변수로 예측한다면,
가령 \(X\): bill_length_mm인 경우, 즉 펭귄의 부리 길이로만 두 종을 분류한다면,

Quadratic discriminant analysis(QDA): 각각을 Gaussian으로 가정하고, 평균과 표준편차를 추정

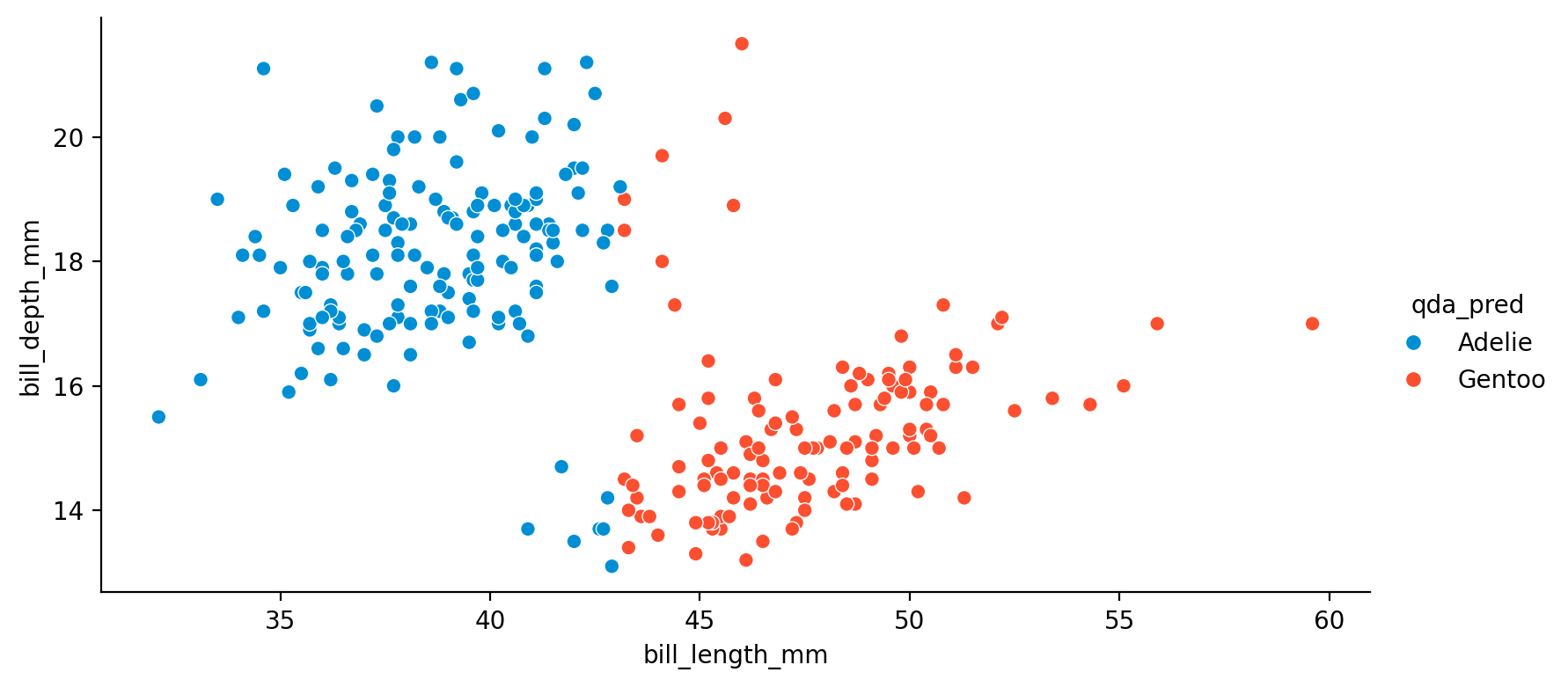
Confusion matrix with the threshold=0.5

Truth      Adelie  Gentoo
Predicted                
Adelie        144       7
Gentoo          7     116

만약, 다음과 같은 loss function (loss matrix)가 주어진다면,

Truth      Adelie  Gentoo
Predicted                
Adelie          0      10
Gentoo         30       0

Expected loss:
\(E(L) = \displaystyle \sum_{i=1} \sum_{j=1} L_{ij}P(y\in C_i, \hat y\in C_j) = \frac{1}{274}(144*0 + 7*10 + 7*30 + 116*0)\)

보통의 경우, 0-1 loss를 사용. 즉, misclassified된 관측치에 대한 비율; misclassification error rate
\(E(L) = \displaystyle \frac{1}{N} \sum_{i=1}^N I(y_i \neq \hat y_i)\) where \(I\) is the indicator function: 0 if \(y_i = \hat y_i\), 1 otherwise

잘못된 예측에 대한 비용이 다르다면, 이에 대응하는 expected loss를 기준으로 모델을 평가

만약, 와인 셀러가 와인의 품질(high:양성 vs. low:음성)을 성분들로 예측하는 모형을 만든다면,
높은 품질의 와인을 낮은 품질로 예측하면, 수익의 악화
- 거짓 음성을 낮춰야 하는 경우: 예를 들어, 영세한 와이너리가 수익이 중요한 경우
낮은 품질의 와인을 높은 품질로 예측하면, 와인 품평가에게 신뢰를 잃을 수 있음
- 거짓 양성을 낮춰야 하는 경우: 예를 들어, 고품질의 와인을 생산하는 것으로 유명한 와이너리; 네임밸류를 유지하기 위해. 반면, 비싼 와인이 싸게 팔리는 것은 감당할 수 있음.

Model evaluation

모델의 평가는 예측함수의 오차로 인한 손실(loss)이 최소인 것으로 기준을 둘 수 있으나,
현실적으로는 모델은 특정 데이터셋, 혹은 특정 관찰값에 의존할 수밖에 없음.

우리가 원하는 것은 관찰값에 대해서가 아닌 일반화된(generalized) 혹은 전체(population)에 대해 손실이 최소이기를 바라는 것임.

전통적 통계에서는 모집단(population)이라는 것을 상정하여, 일반화된 모형을 추론하고자 했음.
- 이를 위해 모집단에 대한 여러 가정들이 필요했으며, 이를 통해 모집단에 대한 추론(inference)을 얻었음.
- 관측치를 최대한 모두 사용하여 모형을 추정하고, 모집단에 대한 추론에 대해 수학적인 수정을 거침.
- Likelihood의 관점에서 최선의 모형을 선택하고, 모집단에 대한 가정을 기반으로 불확성을 추론함.
현대적인 관점에서는 가정없이 관찰된 데이터셋만으로 일반화할 수 있는 다른 접근 방식을 택함.
- 데이터셋을 훈련셋(training set)과 테스트셋(test set)으로 나누어, 훈련셋으로 모델을 구축하고
- 모형이 훈련과정에서 보지 못한 새로운 데이터셋인 테스트셋에서 얼마나 잘 작동하는지를 평가함.
- 이는 모델의 일반화(generalization)가 얼마나 잘 되는지를 평가하는 접근이라고 볼 수 있음.
- 모델의 과적합을 조정하기 위해(bias-variance trade-off) 훈련셋을 다시 여러 개의 서브셋으로 나누어 교차검증(cross-validation)을 수행; 검증셋(validation set)
- 데이터셋에 따라 모델의 파라미터 추정치가 어떻게 바뀌는지를 살펴보기 위해, 부트스트랩(bootstrap)을 사용

훈련셋과 테스트셋에 대한 손실

모형에 대한 평가는 테스트셋에 대한 손실을 기준으로 하고자 함므로, 두 종류의 손실에 대해 구별함.

훈련셋에 대한 손실(오차): 모형을 세우는데 사용된 데이터셋에 대한 손실
테스트/검증셋에 대한 손실(오차): 테스트/검증 데이터셋으로 모형을 평가 했을 때의 손실

모형은 훈련셋에 최대한 적합되도록 세운 것이기 때문에,

훈련셋의 손실(오차) < 테스트/검증셋의 손실(오차)

(단, 모형을 세우는 때 사용된 손실과 동일한 방식의 손실로 평가했을 때)

Resampling methods

Cross-Validation (교차검증)

데이터셋을 훈련셋과 검증셋으로 나누어 보면; validation set approach
예를 들어, Automobile Data(auto) (ISLP 패키지)에서 연비(mpg)를 마력(horsepower)로 예측하는 모델을 만든다면,

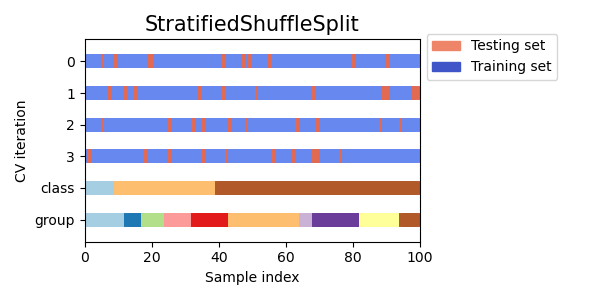
훈련셋과 검증셋을 어떻게 선택하는지에 따라 결과가 바뀜
훈련셋의 양을 얼마나 선택하는지에 따라 결과가 바뀜: 데이터가 작을 수록 모형의 적절성이 낮아짐
아래 그림; 어떻게 데이터셋을 나누느냐에 따라 결과가 달라짐

이를 해결하기 위해 교차검증(cross-validation)을 사용

다수의 훈련셋과 검증셋을 생성하여, 평균값으로 모형의 성능을 평가
다양한 변형이 존재

code

# install ISLP package
# pip install ISLP

from ISLP import load_data
auto = load_data("Auto")
auto.head(3)

    mpg  cylinders  displacement  horsepower  weight  acceleration  year  \
0 18.00          8        307.00         130    3504         12.00    70   
1 15.00          8        350.00         165    3693         11.50    70   
2 18.00          8        318.00         150    3436         11.00    70   

   origin                       name  
0       1  chevrolet chevelle malibu  
1       1          buick skylark 320  
2       1         plymouth satellite

from sklearn.model_selection import train_test_split
auto_train, auto_valid = train_test_split(auto, test_size=.5, random_state=0)

code

p = (
    so.Plot(auto_train, x='horsepower', y='mpg')
    .add(so.Dots(color=".5"))
)
p.show()

for i in range(1, 6):
    p.add(so.Line(), so.PolyFit(i)).label(title=f"M = {i}").show()

Left: Validation error estimates for a single split into training and validation data sets. Right: The validation method was repeated ten times, each time using a different random split of the observations into a training set and a validation set. This illustrates the variability in the estimated test MSE that results from this approach.

Source: p. 204, An Introduction to Statistical Learning with Applications in Python

교차검증의 예

k-fold cross-validation: 데이터셋을 k개의 서브셋으로 나누어, k번의 모형평가를 수행
leave-one-out cross-validation(LOOCV): k=n인 경우
- 거의 모든 데이터로부터 훈련
- k-fold 작업에서 발생하는 무작위성이 없음
Shuffle-split cross-validation: 데이터셋을 무작위로 섞어서 k번의 모형평가를 수행

scikit-learn: Cross-validation 문서 참고

주로 k=5, k=10을 사용; 경험적으로 최적임
- k의 선택에 따라 bias와 variance의 trade-off가 달라짐
- k가 작을수록 variance가 높아지고, bias가 낮아짐

k개의 훈련셋에서 각각에서 얻은 모델에 대해서 검증셋으로부터 모형의 평가치를 얻음: 주로 MSE(mean squared error)

k-fold CV estimate: \(\displaystyle CV_{(k)} = \frac{1}{k} \sum_{i=1}^k MSE_i\)

분류의 경우, misclassification error rate: \(\displaystyle CV_{(k)} = \frac{1}{k} \sum_{i=1}^k \frac{1}{n_i} \sum_{j=1}^{n_i} I(y_j \neq \hat y_j)\)

from sklearn.model_selection import cross_validate, cross_val_score, KFold, ShuffleSplit
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from ISLP import load_data

auto = load_data("Auto")
X = auto[["horsepower"]]
y = auto["mpg"]

cv = KFold(n_splits=10, shuffle=True, random_state=0)

mod_auto = make_pipeline(PolynomialFeatures(2), LinearRegression())  # 2차 다항함수
mod_auto_cv = -cross_val_score(mod_auto, X, y, cv=cv, scoring='neg_mean_squared_error')  # default scoring is R2

print(f"For the quadratic polynomial:\n10-fold Cross-validation \nMSEs: {mod_auto_cv}, \nAverage: {mod_auto_cv.mean()}")

For the quadratic polynomial:
10-fold Cross-validation 
MSEs: [15.98 15.84 18.39 25.88 18.71 23.58 23.58 23.83 11.19 14.88], 
Average: 19.185331419375

code

cv = ShuffleSplit(n_splits=10, test_size=.2, random_state=0)

mod_auto = make_pipeline(PolynomialFeatures(2), LinearRegression())  # 2차 다항함수
mod_auto_cv = -cross_val_score(mod_auto, X, y, cv=cv, scoring='neg_mean_squared_error')  # default scoring is R2

print(f"For the quadratic polynomial:\nShuffle & Spllit Cross-validation with 20% test sets \nMSEs: {mod_auto_cv}, \nAverage: {mod_auto_cv.mean()}")

For the quadratic polynomial:
Shuffle & Spllit Cross-validation with 20% test sets 
MSEs: [16.01 18.34 17.81 12.66 14.97 20.87 13.4  13.62 20.05 15.53], 
Average: 16.32656735042892

code

ev_error1 = np.zeros([10, 10])

X = auto[["horsepower"]]
y = auto["mpg"]

cv = KFold(n_splits=10, shuffle=True, random_state=0)

for i, d in enumerate(range(1, 11)):
    mod_auto = make_pipeline(PolynomialFeatures(d), LinearRegression())
    mod_auto_cv = cross_val_score(mod_auto, X, y, cv=cv, scoring='neg_mean_squared_error')  # cross_validate에 대한 wrapper
    ev_error1[i, :] = -mod_auto_cv

# plot
plt.figure(figsize=(6, 4), dpi=60)
for i in range(10):
    plt.plot(np.arange(1, 11), ev_error1[:, i])
    plt.scatter(np.arange(1, 11), ev_error1[:, i], s=5)

plt.xticks(np.arange(1, 11))
plt.xlabel("Degree of Polynomial")
plt.ylabel("Mean Squared Error")
plt.title("10-fold Cross-validation \nover 10 degrees of Polynomial")
plt.show()

# Shuffle & Split Cross-validation
ev_error2 = np.zeros([10, 10])
cv = ShuffleSplit(n_splits=10, test_size=.2, random_state=0)

for i, d in enumerate(range(1, 11)):
    mod_auto = make_pipeline(PolynomialFeatures(d), LinearRegression())
    mod_auto_cv = cross_val_score(mod_auto, X, y, cv=cv, scoring='neg_mean_squared_error')
    ev_error2[i, :] = -mod_auto_cv

# plot
plt.figure(figsize=(6, 4), dpi=60)
for i in range(10):
    plt.plot(np.arange(1, 11), ev_error2[:, i])
    plt.scatter(np.arange(1, 11), ev_error2[:, i], s=5)

plt.xticks(np.arange(1, 11))
plt.xlabel("Degree of Polynomial")
plt.ylabel("Mean Squared Error")
plt.title("10-split Shuffle & Split Cross-validation \nwith 20% test sets over 10 degrees of Polynomial")
plt.show()

code

ev_error3 = np.zeros([10, 2])

X = auto[["horsepower"]]
y = auto["mpg"]

cv = KFold(n_splits=10, shuffle=True, random_state=0)

for i in range(10):
    mod_auto = make_pipeline(PolynomialFeatures(i+1), LinearRegression())
    mod_auto_cv = cross_val_score(mod_auto, X, y, cv=cv, scoring='neg_mean_squared_error')  # cross_validate에 대한 wrapper
    ev_error3[i, 0] = -mod_auto_cv.mean()

cv = ShuffleSplit(n_splits=10, test_size=.2, random_state=0)

for i in range(10):
    mod_auto = make_pipeline(PolynomialFeatures(i+1), LinearRegression())
    mod_auto_cv = cross_val_score(mod_auto, X, y, cv=cv, scoring='neg_mean_squared_error')  # cross_validate에 대한 wrapper
    ev_error3[i, 1] = -mod_auto_cv.mean()

# plot
plt.figure(figsize=(6, 4), dpi=60)
labels = ["10-fold CV", "10-split Shuffle & Split CV with 20% test set"]
for i in range(2):
    plt.scatter(np.arange(1, 11), ev_error3[:, i], s=5)
    plt.plot(np.arange(1, 11), ev_error3[:, i], label=labels[i])

plt.xticks(np.arange(1, 11))
plt.xlabel("Degree of Polynomial")
plt.ylabel("Mean Squared Error")
plt.title("Average of 10-fold Cross-validation \nover 10 degrees of Polynomial")
plt.ylim(15, 30)
plt.legend(frameon=False)
plt.show()

Scikit-learn: Metrics and scoring

관찰된 데이터에 가장 적합한 모형을 찾는 것이 아니고, 일반화된 모형을 찾는 것이 목표임.
아래 그림에서 관찰된 데이터셋에 대한 예측 오류인 “test error”와 “true error”의 관계를 보여줌.
예를 들어, 아래의 3가지 형태의 true relationship에 대해,

Left: Data simulated from f, shown in black. Three estimates of f are shown: the linear regression line (orange curve), and two smoothing spline fits (blue and green curves). Right: Training MSE (grey curve), test MSE (red curve), and minimum possible test MSE over all methods (dashed line). Squares represent the training and test MSEs for the three fits shown in the left-hand panel.

Source: pp. 29-32, An Introduction to Statistical Learning with Applications in Python

Cross-validation의 test-error가 효과적으로 true error를 반영할 수 있는지를 살펴보면,

보통 실제 test error rate보다 낮게 나오나(즉, 더 적합하게) 최적의 flexibility의 위치는 유사함
참고로, 여기서 true error는 앞서 training/test set으로 나눈 그 test set을 의미하는 것이 아님!

Source: p. 208, An Introduction to Statistical Learning with Applications in Python

다음 절차를 통해, 어떤 클래스의 특정 모델을 선택 후 그 모델의 성능을 평가할 수 있음:

모델 클래스를 선택: 예. linear regression
데이터셋을 traing set과 test set으로 나눈 후,
training set으로 교차검증(sub-trainging & validation sets)을 통해 모델의 flexibility를 결정: 예. 다항식의 차수, tuning parameter 등
- 최적의 flexibility 또는 bias-variance trade off 수준를 결정
최적의 flexibility를 선택한 후, 전체 training set으로 fitting한 모델을 선택 후
test set으로 모델의 성능을 평가

from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.pipeline import Pipeline

auto = load_data("Auto")
X = auto[["horsepower"]]
y = auto["mpg"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.2, random_state=0)

cv = KFold(n_splits=10, shuffle=True, random_state=0)
## Shuffle & Split
# cv = ShuffleSplit(n_splits=10, test_size=.2, random_state=0)

mod_auto = Pipeline([("poly", PolynomialFeatures()), ("lm", LinearRegression())])

# Grid Search
param_grid = {"poly__degree": np.arange(1, 11)}  # "지정한 estimator의 이름"__"parameter 이름"
grid_search = GridSearchCV(mod_auto, param_grid, cv=cv, scoring='neg_mean_squared_error')

grid_search.fit(X_train, y_train)

GridSearchCV(cv=KFold(n_splits=10, random_state=0, shuffle=True),
             estimator=Pipeline(steps=[('poly', PolynomialFeatures()),
                                       ('lm', LinearRegression())]),
             param_grid={'poly__degree': array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10])},
             scoring='neg_mean_squared_error')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# Best parameter!
grid_search.best_params_

{'poly__degree': 10}

# Best estimator!
grid_search.best_estimator_

Pipeline(steps=[('poly', PolynomialFeatures(degree=10)),
                ('lm', LinearRegression())])

grid_search.cv_results_에 교차검증의 여러 지표들이 포함되어 있음

grid_search.cv_results_["mean_test_score"]

array([-24.82, -20.29, -20.37, -20.67, -20.2 , -20.16, -20.4 , -20.49,
       -20.28, -19.94])

grid_search.cv_results_["param_poly__degree"].data

array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=object)

pd.options.display.max_rows = 10
pd.DataFrame(
    {
        "degree": grid_search.cv_results_["param_poly__degree"].data,
        "mean_test_score": -grid_search.cv_results_["mean_test_score"],
    }
).sort_values("mean_test_score")

  degree  mean_test_score
9     10            19.94
5      6            20.16
4      5            20.20
8      9            20.28
1      2            20.29
2      3            20.37
6      7            20.40
7      8            20.49
3      4            20.67
0      1            24.82

2차 다항함수로 충분하다고 판단하고, 전체 training set으로 다시 fitting한 후, test set으로 성능을 평가

mod_auto_best = Pipeline([("poly", PolynomialFeatures(2)), ("lm", LinearRegression())])
mod_auto_best.fit(X_train, y_train)

Pipeline(steps=[('poly', PolynomialFeatures()), ('lm', LinearRegression())])

# get root_mean_squared_error and median_absolute_error
from sklearn.metrics import root_mean_squared_error, median_absolute_error

y_pred = mod_auto_best.predict(X_test)

rmse = root_mean_squared_error(y_test, y_pred)
mae = median_absolute_error(y_test, y_pred)

print(f"Root Mean Squared Error: {rmse:.3f}")
print(f"Median Absolute Error: {mae:.3f}")

Root Mean Squared Error: 4.002
Median Absolute Error: 2.486

The Bootstrap

주어진 데이터셋으로부터 같은 사이즈의 데이터셋들을 중복을 허용해서 추출.
마치 새로운 표본들을 얻는 것과 같은 효과를 얻어, 표본들마다 모형이 어떻게 다르게 추정되는지를 파악함.

예를 들어, 표본에 따라 변하는 파라미터 추정치의 분포를 얻을 수 있음; 파라미터의 불확실성(uncertainty)을 파악
여러 표본에서 학습시킨 모형들을 평균내어 예측력을 높히는데 사용; Bagging (Bootstrap aggregating)
평균적으로 각 표본에서 63.2%의 중복되지 않는 데이터가 선택됨

Sales of Child Car Seats(Carseats) 데이터셋으로 예를 들면,

from ISLP import load_data

carseats = load_data("Carseats")
carseats.head(3)

    Sales  CompPrice  Income  Advertising  Population  Price ShelveLoc  Age  \
0  9.5000        138      73           11         276    120       Bad   42   
1 11.2200        111      48           16         260     83      Good   65   
2 10.0600        113      35           10         269     80    Medium   59   

   Education Urban   US  
0         17   Yes  Yes  
1         10   Yes  Yes  
2         12   Yes  Yes

from sklearn.linear_model import LinearRegression

X = carseats[["Income", "Advertising", "Population", "Price", "Age"]]
y = carseats["Sales"]

# linear regression
lm_carseats = LinearRegression()
lm_carseats.fit(X, y)

LinearRegression()

params = pd.DataFrame(lm_carseats.coef_, index=X.columns, columns=["params"])
params

             params
Income       0.0107
Advertising  0.1254
Population  -0.0009
Price       -0.0574
Age         -0.0490

from sklearn.utils import resample

np.random.seed(0)
params_boot = params.copy()

for i in range(1000):
    X_new, y_new = resample(X, y, replace=True)  # resampling with replacement
    lm_carseats.fit(X_new, y_new)  # refit
    
    params_new = pd.DataFrame(lm_carseats.coef_, index=X.columns, columns=[f"sample_{i}"])
    params_boot = pd.concat([params_boot, params_new], axis=1)

params_boot

             params  sample_0  sample_1  sample_2  sample_3  ...  sample_995  \
Income       0.0107    0.0037    0.0175    0.0126    0.0100  ...      0.0139   
Advertising  0.1254    0.1439    0.1170    0.1158    0.1232  ...      0.1392   
Population  -0.0009    0.0001   -0.0019   -0.0007   -0.0012  ...      0.0008   
Price       -0.0574   -0.0630   -0.0462   -0.0552   -0.0595  ...     -0.0630   
Age         -0.0490   -0.0595   -0.0404   -0.0574   -0.0465  ...     -0.0478   

             sample_996  sample_997  sample_998  sample_999  
Income           0.0113      0.0082      0.0132      0.0063  
Advertising      0.0914      0.0904      0.1221      0.1253  
Population      -0.0016     -0.0002     -0.0018     -0.0002  
Price           -0.0558     -0.0518     -0.0512     -0.0469  
Age             -0.0486     -0.0535     -0.0394     -0.0375  

[5 rows x 1001 columns]

1000개 표본에서 파라미터 추정치의 표준편차; standard error

params_boot.std(axis=1)

Income        0.0038
Advertising   0.0174
Population    0.0008
Price         0.0050
Age           0.0069
dtype: float64

실제 파라미터 추정치의 분포를 보면,

params_boot.T.hist(bins=30, alpha=.7, figsize=(7, 3), layout=(2, 3))
plt.tight_layout()
plt.show()

이 분포로부터 파라이터 추정치의 confidence interval (신뢰구간)을 구할 수 있음; 여러 변형이 존재함.
보통 95% 신뢰구간을 사용

Short version

np.random.seed(0)

params = pd.Series(lm_carseats.coef_, index=X.columns)
err = np.std([lm_carseats.fit(*resample(X, y)).coef_ for i in range(1000)], axis=0)

pd.DataFrame({'coef': params, 'error': err})

#                coef  error
# Income       0.0063 0.0038
# Advertising  0.1253 0.0174
# Population  -0.0002 0.0008
# Price       -0.0469 0.0050
# Age         -0.0375 0.0069

선형회귀에서 OLS estimation 결과와 비교하면,

from statsmodels.formula.api import ols

lm_carseats2 = ols("Sales ~ Income + Advertising + Population + Price + Age", data=carseats).fit()

print(lm_carseats2.summary(slim=True))

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                  Sales   R-squared:                       0.373
Model:                            OLS   Adj. R-squared:                  0.365
No. Observations:                 400   F-statistic:                     46.82
Covariance Type:            nonrobust   Prob (F-statistic):           6.07e-38
===============================================================================
                  coef    std err          t      P>|t|      [0.025      0.975]
-------------------------------------------------------------------------------
Intercept      15.4227      0.808     19.098      0.000      13.835      17.010
Income          0.0107      0.004      2.635      0.009       0.003       0.019
Advertising     0.1254      0.018      7.112      0.000       0.091       0.160
Population     -0.0009      0.001     -1.086      0.278      -0.002       0.001
Price          -0.0574      0.005    -11.962      0.000      -0.067      -0.048
Age            -0.0490      0.007     -7.000      0.000      -0.063      -0.035
===============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.37e+03. This might indicate that there are
strong multicollinearity or other numerical problems.